 The free pendulum is the one-degree of freedom Hamiltonian system
where x is the angle to the force of gravity,
y is the angular velocity and g depends on
the length of the pendulum and gravitational field strength.
The energy of the pendulum
The free pendulum is the one-degree of freedom Hamiltonian system
where x is the angle to the force of gravity,
y is the angular velocity and g depends on
the length of the pendulum and gravitational field strength.
The energy of the pendulum
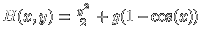 is also called the Hamiltonian of the system. It is a sum
of the kinetic energy
K(y)=y2/2 and the potential energy
V(x) = g (1-cos(x)). The equation of motions are
the Hamilton equations
is also called the Hamiltonian of the system. It is a sum
of the kinetic energy
K(y)=y2/2 and the potential energy
V(x) = g (1-cos(x)). The equation of motions are
the Hamilton equations
 Because energy is conserved:
Because energy is conserved:
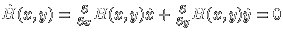 , and of one degree of freedom,
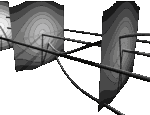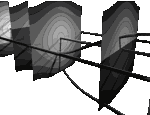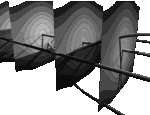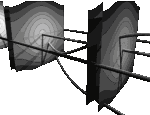
the system is integrable: any solution
(x(t),y(t)) in the cylindrical phase space is either periodic,
stationary at one of the equilibrium situations , and of one degree of freedom,
the system is integrable: any solution
(x(t),y(t)) in the cylindrical phase space is either periodic,
stationary at one of the equilibrium situations
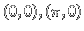 , or asymptotic to the equilibrium
situation , or asymptotic to the equilibrium
situation 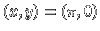 , where the pendulum tops.
Explicit formulas for (x(t),y(t)) use elliptic integrals. , where the pendulum tops.
Explicit formulas for (x(t),y(t)) use elliptic integrals.
|
 The free pendulum is the one-degree of freedom Hamiltonian system
The free pendulum is the one-degree of freedom Hamiltonian system
 Because energy is conserved:
Because energy is conserved:
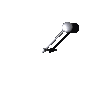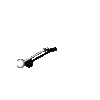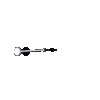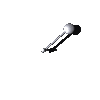 The free pendulum is the one-degree of freedom Hamiltonian system
The free pendulum is the one-degree of freedom Hamiltonian system
 Because energy is conserved:
Because energy is conserved:
 Hamiltonian systems driven by a
Hamiltonian systems driven by a