The Stoermer Problem

The motion of a charged particle in a magnetic dipole-field is today called the Stoermer problem. Since a long time, physicists and mathematicians have in the context of the northern lights and cosmic radiation been interested how a charged particle moves in the magnetic field of the earth. The problem has turned out to be difficult. After decades of searching for an additional integral besides the energy and the angular momentum, one has realized that the problem is not integrable. A model problem of Brown which simulates a Poincare return map has indeed been shown to have a horse shoe.

be a rotational symmetric vector potential in cylinder coordinates This vector potential generates a magnetic field which is rotational symmetric. The Hamiltonian system of the Störmer problem describes the motion of a single charged particle of charge q, mass m and velocity v in the magnetic dipole field B. This is a sketch. For more details see Alex Dragt, Trapped orbits in a magnetic dipole field; Rev. of Geophys.3(2) (1965), pp.255-298 and More literature. [Added August 6, 2012: Thanks to Sateesh R. Mane for some corrections on this page]. Let $A= (0,0,A_z) = (0,0,M \rho r^{-3})$ be a rotational symmetric vector potential in cylinder coordinates $(\rho,\phi,z)$ , where $\rho$ is the distance from the dipole axes, which is the z-axes and where $r=r(\rho,z)$ is the distance from the dipole which is located at the origin. M is the magnetic dipole moment of the field.

This vector potential generates a magnetic field $B = \nabla \wedge A = {\rm curl}(A) = (0,-\partial A_z/\partial \rho,0)$ , which is rotational symmetric. The Hamiltonian system of the Störmer problem describes the motion of a single charged particle of charge q, mass m and velocity v in the magnetic dipole field B.

The relativistic Hamilton function of the particle is in cylinder coordinates given by

$\begin{displaymath}K = \left(m^2 c^4 + c^2 p_z^2 + c^2 p_{\rho}^2 + c^2 (p_{\phi}/\rho-qA_{z})^2 \right)^{1/2} = \gamma m c^2 \; , \end{displaymath}$

where c is the speed of light, $\gamma = (1-v^2/c^2)^{1/2}$ , and $(p_z,p_{\rho},p_{\phi}) =\gamma m(\dot{z},\dot{\rho}, \dot{\phi} \rho^2+q \rho A_z)$ .

Because v² and so $\gamma$ are constants of motion, one can introduce a new Hamilton function H, equivalent to K, which has the form of a non-relativistic Hamiltonian:

$\begin{displaymath}H = \frac{1}{2 \gamma m} \left(p_z^2 + p_{\rho}^2 + (p_{\phi}+q A_z)^2 \right) = \frac{1}{2} \gamma m v^2 \; , \end{displaymath}$ .

The equivalence of the two Hamilton function K and H can be seen by observing that the partial derivatives with respect to all dynamical variables agree.
Because H is invariant under the one-parameter group of rotations along the z axes, there is by Noether's theorem an integral $\dot{\phi} = - \partial H/\partial \phi = 0$ so that $p_{\phi} = q M \Gamma$ , where $\gamma$ has the dimension of a inverse length.
After elimination of the variable $\phi$ , one has the problem to determine the motion of a particle in the $\rho-z$ plane, which moves under the potential V:

$\begin{displaymath}V(\rho,z) = \frac{q^2 M^2}{2 \gamma m} \left( \frac{\Gamma}{\rho} - \frac{\rho}{r^3} \right) \; . \end{displaymath}$

After introducing dimensionless variables $z'=\Gamma z, \rho' = \Gamma \rho, \phi' = \phi, t' = \Gamma^3 q M \gamma m^{-1} t$ and leaving away the apostrophes, the Hamilton function becomes

$\begin{displaymath}H = \frac{1}{2}( p_z^2 + p_{\rho}^2 ) + \frac{1}{2}( \frac{1}{\rho} - \frac{\rho}{r^3} )^2 = \frac{1}{32 \gamma_1^4} \; , \end{displaymath}$

where $\gamma_1$ is the Störmer constant $\gamma_1^4 = \frac{1}{16} (\frac{q M}{v \gamma m})^2 \Gamma^4$ .

The potential V vanishes on the 'Thalweg' $\rho^2=r^3$ which is the minimum of the elsewhere positive potential. For $\gamma_1>1$ , the allowed region of the particle is not connected and we are especially interested in the motion of the compact connected region. The motion in the unbounded region is integrable by an observation of Moser. The asymptotic velocities of the escaping particles provide the integrals of motion.

The Störmer problem is to analyze the two degree of freedom Hamiltonian system with Hamiltonian

$\begin{displaymath}H(q_1,q_2,p_1,p_2) = \frac{1}{2} (p_1^2+p_2^2) + \frac{1}{2} (\frac{1}{q_1} - \frac{q_1}{(q_1^2+q_2^2)^{3/2}})^2 \; , \end{displaymath}$

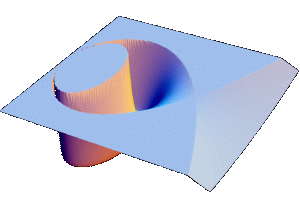The energy surface H(q,p)=E with 0<E<1/32 contains a compact component on which the flow is area preserving. The two dimensional hyper-surface q₁=0 in the energy surface is a Poincaré surface and the ruturn map is a symplectic map. The second iterate of this return map can be written as a composition of integrable twist maps. The first map is to shoot the particle from q₂=0 to the north (with p₂>0) and wait until it comes back. The second map is to shoot the particle from q₂=0 to the south and wait until it comes back to the equator q₂=0. Both maps are twist maps in the plane which have a single fixed point which is the initial condition which shoots the particle into the dipole. That this map is integrable has been shown by finding a regularization of the motion near the singularity of the dipole. The two fixed points of the two maps do not agree, the two maps don't commute. When shooting to the north pole, the particle will not bounce back to the south pole. The situation is similar to take a two horn-like surfaces of revolution and glue them together a bit tilted, leading to a two dimensional surface of revolution with one line, where the metric is discontinuous. Writing this in Texas, it is a Longhorn, the left horn representing the charged particle on the north hemisphere, the right horn representing the charged particle on the south hemisphere. The geodesic flow on this surface of revolution is a Hamiltonian system which is very similar to the Hamiltonian system of the Störmer problem.

The Katok-Strelcyn conditions required for Pesin theory are satisfied. An open problem is to establish positive Kolmogorov-Sinai entropy. One would have to show the positivity of the Lyapunov exponent on a set of positive Lebesgue measure.

The Stoermer Problem

Some weblinks to the Stoermer Problem