Bouncing ball particle system

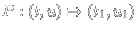bouncing ball A particle bouncing between a fixed and an oscillating wall is an example of a dynamical system which shows a mixture of regular and chaotic behavior. One can study this dynamical system through a Poincaré map P: (t,u) -> (t_1,u_1). The variable u is the speed of the particle just before hitting at time t the wall in position cos(t). The image point is determined by the speed u1 of the particle when it leavs the wall the next time t1. 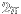The time variable is taken modulo 2\pi so that P is an area-preserving map of the half-cylinder X = { (t,u), t mod 1, u > 0 }.
The return map P is smooth on X if one assumes that the moving wall imparts momentum ( - sin(t)) to the ball but stays at a fixed position. Let l be the average distance between the fixed and moving wall and let v the speed of the particle. Assuming no gravity, an approximation to P is
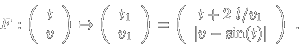(t,v) -> (t1,v1) = (t+ 2\; l/v_1, |v-sin(t)|
This simplified Fermi map is the composition of two maps, the instantaneous velocity gain 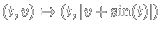F: (t,v) -> (t, |v+sin(t) |) at the impact time t and the following free motion 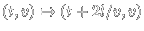(t,v) -> (t+2l/v,v) until the next impact.
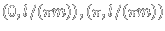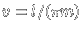The fixed points $(0,l/(\pi m)),(\pi,l/(\pi m))$ of F are labeled by a positive integer m. They correspond to initial speeds which lead to a periodic return after m floor-oscillations, hitting when the floor is at a lowest rsp. highest point (the animation on this page is such a fixed point with m=1). A linearization in the variable v near $v=l/(\pi m)$ using 1/(v+u) = 1/v - 1/v2 u + O(u 2) leads to the map
S: (t,u) -> (t - gamma u_1, u - sin(t) )
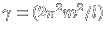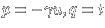with parameter $\gamma = (2 \pi^2 m^2/l)$. After a change of variables $p = - \gamma u, q=t$, this is
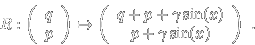R: (q,p )) -> (q+p+gamma sin(x), p+gamma sin(x)
which is conjugated by the discrete involutive Legendre transformation (x,y)=(-q,p-q) to the Standard map
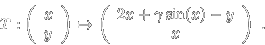
T: (x,y) -> (2x-y+gamma sin(x),x)

Animation Webtechnical information on these pages


© 1999, Oliver Knill , dynamical-systems.org