Periodically Driven Pendulum

Pendulum The free pendulum is the one-degree of freedom Hamiltonian system
d/dt x = y, d/dt y = g sin(x)
where x is the angle to the force of gravity, y is the angular velocity and g depends on the length of the pendulum and gravitational field strength. The energy of the pendulum 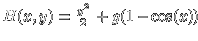H(x,y) = y^2/2 + g (1-\cos(x) is also called the Hamiltonian of the system. It is a sum of the kinetic energy K(y)=y2/2 and the potential energy V(x) = g (1-cos(x)). The equation of motions are the Hamilton equations
d/dt x = d/dy H(x,y), d/dt y = - d/dx H(x,y)
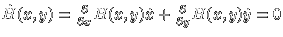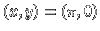Zylindrical phase space of pendulum foliated by energy leaves Because energy is conserved: $d/dt H(x,y) = d/dx H(x,y) d/dt x + d/dy H(x,y) d/dt y = 0, and of one degree of freedom, the system is integrable: any solution (x(t),y(t)) in the cylindrical phase space is either periodic, stationary at one of the equilibrium situations (0,0),(\pi,0), or asymptotic to the equilibrium situation (x,y)=(pi,0), where the pendulum tops. Explicit formulas for (x(t),y(t)) use elliptic integrals.
A periodically driven pendulum is a system
d/dt x = y, d/dt y = g sin(x) + f(t,x),
where f(t,x) is an external force which is periodic in t. A possible physical realization is a pendulum containing a magnet influenced by a second magnet which rotates with uniform speed. Hamiltonian systems with 1 1/2 degrees of freedom can have complicated dynamics. The energy H(x,y) is no more constant.
Poincare map Hamiltonian systems driven by a \tau -periodic force can be studied with the map T: (x(0),y(0)) -> (x(\tau),y(\tau)). This Poincaré map is an area-preserving map of the cylinder which captures all essential properties of flow determined by the differential equation.
For a given system, one is interested in questions like whether there are orbits for which the energy becomes unbounded, in finding and classifying periodic orbits, finding invariant sets on which the dynamics is quasiperiodic (i.e. near elliptic periodic orbits or for large velocity) or sets on which the dynamics is conjugated to a Bernoulli shift (i.e. when stable and unstable manifolds of a hyperbolic periodic point intersect transversely). Of quantitative interest is the Lyapunov exponent lambda(x,y)=limsup_{n to infinity} log || dT^n(x,y) ||, where Tn(x,y)=T(Tn-1(x,y)) is the orbit and dS(x,y) denotes the Jacobean matrix of a map S. When the Lyapunov exponent is averaged over a bounded T-invariant set of initial conditions, it gives the entropy of a part of the system.

Animation Webtechnical information on these pages


© 1999, Oliver Knill , dynamical-systems.org