No Title

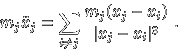
The three body problem

The equations of motion
A central topic in celestial mechanics is the study of the Newtonian n-body problem

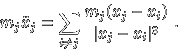
$\begin{displaymath}m_j \ddot{x}_j = \sum_{i \neq j} \frac{m_j (x_j-x_i) }{\vert x_j-x_i\vert^3} \; . \end{displaymath}$

The phase space of this system of ordinary differential equations is T^*M with $M={\bf R}^{3 n} \setminus \Delta$ , where $\Delta = \bigcup_{i \neq j} \Delta_{ij} = \bigcup_{i \neq j} \{ x \in {\bf R}^{3n} \; \vert \; x_i = x_j \; \}$ is the set of collisions. With the real analytic Hamiltonian $H: T^*M \to {\bf R}$ , $H(x,y) = \sum_{j=1}^n \frac{1}{2m_j} y_j^2 + U(x)$ , $U(x) = - \sum_{i < j} \gamma \frac{m_i m_j}{\vert x_i-x_j\vert}$ . For $\gamma=1$ , the Newton equations are the Hamilton equations $\dot{x}_j = \frac{\partial}{\partial y_j} H(x,y)$ , $\dot{y}_j = - \frac{\partial}{\partial x_j} H(x,y)$ . If $\gamma=-1$ , one has the Coulomb system, in which case particles repell each other and where the energy is always positive. In ${\bf R}^n$ with n > 2, the Newton potential is $U(x) = - \sum_{i < j} \gamma m_i m_j (\vert x_i-x_j\vert^{-(n-2)}$ . For n=2, the natural potential is $U(x) = - \gamma \sum_{i < j} m_i m_j \log \vert x_i-x_j\vert$ . In dimension n, the force is $\gamma (x_i-x_j) \vert x_i-x_j\vert^{-n}$ . A regularisation of the singular potential is obtained by replacing |x|^-nby $(x^2+\epsilon)^{-n/2}$ .

Integrals
The N-body problem in n dimension has (n²+3n+2)/2 classical integrals of motion: n from the total momentum, n from the position of the center of mass, and n (n-1)/2 from the total angular momentum $L(x,y)=\sum_i x_i \wedge y_i$ (because $\dot{L}=\sum_i \dot{q}_i \times p_i + \sum_i q_i \times \dot{p}_i$ is zero using $q_i \times (q_i -q_j)=-q_i \times q_j$ ) and finally, 1 from the energy H(x,y). Because 2nN-1 integrals of motion were necessary to integrate the N-body problem, there are in general not enough classical integrals if N>2. Already the Newtonian 3-body problem in n=2 contains all the complexity a dynamical system can have.

Rough history
Before Newton, the dynamics of celestial objects was described empirically which means that laws were drived from observations. Examples are Kepler's laws. Newton found the laws for classical dynamics and developed differential and integral calculus simultaneously with Leibnitz. This allowed him to prove Kepler's laws from more fundamental principles. Laplace, Lagrange and Poisson belong to the ancestors of celestial mechanics. With Poincaré at the end of the last century and Birkhoff in the twenties of this century, the subject was studied with new geometric and topological methods. Geometrical methods are involved for example when studying singularities, energy surfaces, equilibrium configurations, invariant manifolds. Topological methods are invoked for example when proving the existence of solutions through fixed point theorems. In the middle of the 20'th century, probabilitistic tools from ergodic theory and statistical mechanics have been invoked. Ergodic theory deals with the structure of invariant measures and the measure-preserving flows, when an invariant probability measure is present. In statistical mechanics, one is interested in the evolution of measures on the Fock space of classical mechanics or in limits, when the particle number goes to infinity. In the second half of this century, progress on stability questions has been achieved with perturbative methods. Newer renormalisation proofs of stability also suggest universal behavior can be relevant in n-body problems, when parameters like masses are changed. The study of periodic orbits using variational and topological index methods became a subject in itself. Subquestions include the study of the stability of orbits or bifurcations depending on parameters and other questions related with universality. Other minimal systems coming from subshifts or quasiperiodic motion on Cantor set were found by variational, perturbative or geometric arguments. Partial differential equations enter when the formalism is extended to Vlasov dynamics, a more general dynamical system which allows to evolve more general measures like smooth densities. The corresponding evolution equation, the Vlasov equation is fundamental in stellar dynamics and contains as a special case of discrete measures the n-body problem. Stability of equilibria solutions or qualitative analysis of the evolution are quite modern topics of research. Noncollision singularities of the Newtonian n-body problem in three dimensions have been found by Xia (n=5) and Gerber (large n). While it is known that collision singularities have Lebesgue measure zero and are Baire meager it is now known whether the Newtonian n-body problem has global solutions for almost all initial conditions. This is one of the important open problems in celestial mechanics.

Research topics Research on n-body problems can include

A formal understanding the laws governing the n-body problem consists of finding integrals, reduction using symmetry, numerical investigation of solutions or perturbative computations.
Existence of special solutions like periodic, quasiperiodic or random motions. Determination of the stability of solutions the structural stability of the system. Classifying invariant measures.
See the global structure of solutions, understanding singularities with adequate coordinate systems, understand the set of collisions and noncollision singularities, i.e. their size. Understand the set of initial conditions leading to bounded motions.
Study of related systems, particle systems on more general manifolds, in other dimensions, in regions with boundary, with other interactions, restricted n-body problems.
Statistical properties, entropy, large number of particles (i.e. galaxy dynamics), Vlasov generalization i.e. infinite particle cases, the study of BBGKY with methods of partial differential equation. Addition of white noise leads to quantum dynamics.

Literature
Good starting points in the literature of n-body problems are

Bibliography

1: R. Abraham and J. Marsden.
Foundations of Mechanics.
Benjamin and Cummings Publishing Company, London, 1978.
2: V. I. Arnold, V. V. Kozlov, and A. I. Neishtadt.
Mathematical aspects of classical and celestial mechanics.
Springer-Verlag, Berlin, 1997.
3: V.I. Arnold.
Mathematical problems in classical physics.
In L. Sirovich, editor, Trends and Perspectives in Applied Mathematics. Springer-Verlag, New York, 1994.
4: June Barrow-Green.
Poincaré and the three body problem.
American Mathematical Society, 1997.
5: J. Binney and S. Tremaine.
Galactic dynamics.
Pinceton Series in Astrophysics. Pinceton University Press, Princeton 1987, 1987.
6: C.L.Siegel and J.K.Moser.
Lectures on Celestial Mechanics.
Grundlehren der mathematischen Wissenschaften. Springer Verlag, Berlin, 1971.
7: H. S. Dumas, K. R. Meyer, and D. S. Schmidt, editors.
Hamiltonian dynamical systems.
Springer-Verlag, New York, 1995.
History, theory, and applications, Papers from the International Conference held at the University of Cincinnati, Cincinnati, Ohio, March 1992.
8: J. Moser.
Dynamical systems-past and present.
In Proceedings of the International Congress of Mathematicians, Vol. I (Berlin, 1998), volume 1998, pages 381-402.
9: J. Moser.
Stable and random Motion in dynamical systems.
Princeton University Press, Princeton, 1973.
10: Henri Poincaré.
New methods of celestial mechanics. Vol. 1.
American Institute of Physics, New York, 1993.
Periodic and asymptotic solutions, Translated from the French, Revised reprint of the 1967 English translation, With endnotes by V. I. Arnold, Edited and with an introduction by Daniel L. Goroff.

Animation