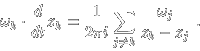
Vortex motion

The motion of N vortices with voriticity $\omega_i$ located at points z_i in the complex plane ${\bf C}$ is determined by the differential equations

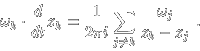
$\begin{displaymath}\omega_k \cdot \frac{d}{dt} \overline{z_k} = \frac{1}{2 \pi i} \sum_{j \neq k} \frac{\omega_j}{z_k-z_j} \; . \end{displaymath}$

This is a Hamiltonian system

$\begin{displaymath}\omega_k \dot{x}_k = \frac{\partial H}{\partial y_k}, \omega_k \dot{y}_k =-\frac{\partial H}{\partial x_k} \end{displaymath}$

for the variables x_i+i y_i=z_i. The Hamiltonian function or energy is

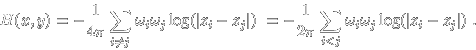
$\begin{displaymath}H(x,y)=-\frac{1}{4\pi} \sum_{i \neq j} \omega_i \omega_j \log... ...} \sum_{i < j} \omega_i \omega_j \log(\vert z_i-z_j\vert) \; . \end{displaymath}$

Using the notation $\frac{\partial}{\partial z_k} =\frac{1}{2} (\frac{\partial}{\partial x_k} - i \frac{\partial}{\partial y_k})$ one can write

$\begin{displaymath}\omega_k \cdot \frac{d}{dt} \overline{z}_k = \frac{2}{i} \frac{\partial H}{\partial z_k} \; , \end{displaymath}$

the variables $q_i=\omega_i x_i, p_i=y_i$ are canonically conjugated. The phase space of the system is $D={\bf C}^{N} \setminus \Delta$ , where $\Delta=\bigcup_{1 \leq i \leq j \leq N} \{z_i=z_j \}$ is the collision set.

The N vortex system has 4 classical integrals of motion: two integrals for the center of mass $Z=Q+iP=\sum_i \omega_i z_i$ , one integral for the angular momentum $I=\sum_i \omega_i \vert z_i\vert^2$ and one integral for the energy H. The center of mass is invariant because every term in $\sum_i \omega_i \dot{z}_i$ appears twice with opposite sign. To see the angular momentum invariance, define $S= \sum_k \omega_k z_k \overline{\dot{z}}_k$ Because I and $\dot{I}$ are real, $\dot{I}=S+\overline{S}$ holds and

$\begin{displaymath}\dot{S}= \frac{1}{2\pi i} \sum_{k \neq j} \frac{\omega_k \o... ...z_k-z_j} = \frac{1}{2\pi i} \sum_{k \neq j} \omega_k \omega_j \end{displaymath}$

is purely imaginary so that $\dot{I}=S+\overline{S}=0$ . The energy is invariant because $\dot{H}=\sum_i H_{x_i} \dot{x}_i + H_{y_i} \dot{y}_i =\sum_i H_{x_i} H_{y_i} \omega_i^{-1} - H_{y_i} H_{x_i}\omega_i^{-1} = 0$ . These integrals come from symmetry: the translational, rotational and time invariance of the differential equations. With the Poisson bracket

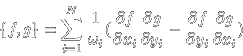
$\begin{displaymath}\{ f,g \} =\sum_{i=1}^N \frac{1}{\omega_i} ( \frac{\partial ... ...ac{\partial f}{\partial y_i} \frac{\partial g}{\partial x_i} ) \end{displaymath}$

for two smooth functions $f,g: {\bf C}^N \rightarrow {\bf C}$ , the notation $\partial_z=\frac{\partial}{\partial z} = \frac{1}{2} (\partial_x-i \partial_y)$ and the scalar product $<u,v>={\rm Re}(u \cdot \overline{v})$ on ${\bf C}$ one has

$\begin{displaymath}\{ f,g \} = \sum_i \frac{4}{\omega_i} < \partial_{z_i} f, i \partial_{z_i} g > , \end{displaymath}$

and the equations of motion are $\dot{z}_i= \{ z_i,H \}$ or

$\begin{displaymath}\dot{x}_i = \{ x_i,H \}, \; \dot{y}_i=\{ y_i,H\} \; . \end{displaymath}$

The invariance of the integrals means $\{I,H\}=\{Z,H\}=0$ . Other integrals are obtained by combining known ones. For example $J:=\frac{1}{2} \vert Z\vert^2= \frac{1}{2} (P^2+Q^2)$ is an integral.

Because H,I,J have pairwise non-vanishing Poisson brackets, a 3 vortex system is explicitly integrable. The threshold for chaotic behavior starts with N=4. Already the restricted 4-vortex system is non-integrable. It is the limiting case, where one of the vortices does not contribute to the vorticity.

If the vorticities are positive and $z \in D$ , the solution of the vortex flow exists for all times because $I=\sum_i \omega_i \vert z_i\vert^2 = const$ defines a compact set and because H=const prevents collisions.

If $\omega_i$ takes both signs the existence and uniqueness problem is nontrivial and catastrophes are possible: the 3-vortex situation $z_1=(-1,0),z_2=(1,0), \omega_1=\omega_2=2$ and $z_3=(1,\sqrt{2})$ $\omega_3=-1$ for example leads to a collapse at time $t=3 \sqrt{2} \pi$ : if a_i are the lengths of the triangle formed by z₁,z₂,z₃and A is the triangle area, one has $\frac{d}{dt} a_k^2 = \frac{2 \omega_k A}{\pi} (\frac{1}{a_{k-1}^2} - \frac{1}{a_{k+1}^2} )$ . The ratios of the triangle lengths are conserved implying $\frac{d}{dt} a_k^2 = - \frac{1}{3 \sqrt{2} \pi} a_k^2(0)$ so that $a_k(t)=a_k(0) \sqrt{1-\frac{t}{3 \sqrt{2} \pi}}$ .

Kolmogorov-Arnold- Moser theory implies that there exists always quasi-periodic motion in the phase space of a N-vortex system. A vortex system of four or more vortices shows therefore a mixture of stable and unstable behavior.

Animation

Webtechnical information on these pages