|
|
You can numerically determine here
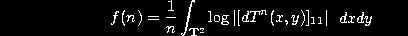 , where T is the Chirikov Standard map
T(x,y) = (2x-y+k sin(x),x).
The sequence f(n) converges in the limit n
to infinity to the Kolmogorov-Sinai entropy of the map (Pesin formula).
The conjecture is that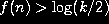 
for all k and all n>0.
(m determines the accuracy of
the Riemann sum approximating the integral over the phase space.
The program sums over a (m x m)-grid in the phase space.) Every 5 runs,
your experiment results are submitted to our database. The computation
done on your computer will so help to test the hypothesis. This is also
an experiment in distributed computing.
|
|
|
